   |
|
|
| |
|
|
|
|
 |
Angelo Capasso
|
|
|
NOTES ON A MATHEMATICS OF SENSATION
|
|
|
|
“I am able to prove that not
only light, colour, and the like, but also movement, shape,
and space are all nothing but apparent qualities”
LEIBNIZ
|
“I only use numbers because
it is a way of writing without describing”
HANNE DARBOVEN |
NUMBERS.
Sensual and optical realities both hide a common question:
their apparent solidity. What represents the concrete
character of sight, of feeling, of smell, when compared with
the logical process with which we qualify our quantitative
presence in the world? Every process is enumerable. Numbers
are that necessary instrument for defining a thought which
processes the Infinite. In order to accept a mathematical
description of nature, physicists were forced to abandon the
common world of experience, the world of the perception of
the senses. To understand the meaning of this abandonment,
we must go beyond that fragile boundary that divides physics
from mathematics. Art, whenever it has to do with numbers,
when it flaunts its structural version, can be the mobile
threshold through which we link quality and quantity by way
of the iconic value of numbers. The number takes on the part
of the main character with the Avantgardes. It enters into
the picture, into the painting itself, into the collage,
into the installation, it enters into the system of exchange
and hardens as irreplaceable thought in order to understand
the speed and progress of chance. As in the comparison
between physics and mathematics, art has posed queries able
to understand the relationships between observer and reality,
between subject and object, in other words it has placed
those questions – that have tormented philosophers since the
dawn of reason, since the original cyphers were still
immersed in the nebula of original experience – onto a
visual level.
|
 |
1.
Euclid and Fibonacci: numeral space
Euclidean space is an axiomatic one. His own form of
geometry which is based on certain commonly-shared notions
that are accepted as postulates, has produced elementary
theorems, upon which even today we base minimalist,
rationalistic, naturalistic thought: the ‘correct way of
thinking’ (which he calls the rules of inference), are posed
as if provided by propositions whose truth is accepted
without any demonstration. The propositions (the axioms) act
as starting-point from where we rigorously demonstrate (using
the rules of inference) all that follows (the theorems).
|
2.
Artists, engineers and architects:
Leonardo da Vinci and Piero della Francesca.
Leonardo da Vinci noted that the numbers of Fibonacci
matched the position of leaves upon different types of plant,
or rather phyllotaxis. That progression corresponded to the
golden proportion. The French painter, Seurat, made
conscious use of it in many of his works. Use of the numbers
of Fibonacci are to be seen in the “fugues” of Johannes
Sebastian Bach, in the Sonata in A D959 by Schubert, in some
of the works of Debussy and Ravel, in the Allegro Barbaro of
Béla Bartók.
|

ALIGHIERO BOETTI |
3.
Game and chaos in the case of
Dada
Every puzzle is a question of putting things together. If a
single piece is missing, the whole system goes mad. A
child’s room is in a state of chaotic orderliness which he
elaborates by adding chaos to chaos. Jean Arp let shapes
fall on to a surface and studied their relationships.
 |

GINO DE DOMINICIS |
|
4.
Numbers and letters:
surrealist science
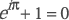
The formula of Euler, a great Swiss mathematician of the
18th century, establishes an apparently amazing relationship
between certain constants of universal usage: at first sight
it would seem indeed very strange that (a transcendent
number raised to the imaginary unit and multiplied by
another transcendent number) could be equal to –1. It is
precisely in this transcendent relation that that equation
permits the greatest paradox.
|
5.
Florensky and De Chirico: the
experience of the sacred and of the enigma
The metaphysical experience brings about infinite unity.
Numbers signal the interpretations of the symbol. The number
One mirrors itself and in such a way, coming back to itself,
comes true like a new One, which is Two and so gradually
becomes all the successive numbers. Just like in the
obsessive repetitions of Warhol, repetition produces a
harmony which frees the shape from the contents.
|
|
|
|
|